Subconjuntos próprios e impróprios 

             Se e são conjuntos e todo o elemento pertencente a também pertence a , então o conjunto é dito um subconjunto do conjunto , denotado por . Note que esta definição inclui o caso em que e possuem os mesmos elementos, isto é, são o mesmo conjunto (). Se e ao menos um elemento pertencente a não pertence a , então é chamado de subconjunto próprio de , denotado por . Todo conjunto é subconjunto dele mesmo, entretanto não se enquadra na definição de subconjunto próprio, e é chamado de subconjunto impróprio.

 Conjunto vazio

 

 

        Todo conjunto também possui como subconjunto o conjunto vazio representado por { } ou .

Podemos mostrar isto supondo que se o conjunto vazio não pertence ao conjunto em questão, então o conjunto vazio deve possuir um elemento ao menos que não pertença a este conjunto. Como o conjunto vazio não possui elementos, isto não é possível. Como todos os conjuntos vazios são iguais uns aos outros, é permissível falar de um único conjunto sem elementos.

Cardinalidade

         Se um conjunto tem n elementos, onde n é um número natural (possivelmente 0), então diz-se que o conjunto é um conjunto finito com uma cardinalidade de n ou número cardinal n.

Mesmo se o conjunto não possui um número finito de elementos, pode-se definir a cardinalidade, graças ao trabalho desenvolvido pelo matemático Georg Cantor. Neste caso, a cardinalidade poderá ser 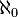(aleph-0), .

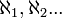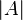Nos dois casos a cardinalidade de um conjunto é denotada por . Se para dois conjuntos A e B é possível fazer uma relação um-a-um entre seus elementos, então .